c逆向之除法 • 🥳🎉你发现了一个有趣的网站

除数为2的n次幂时

结论：

对于无符号的被除数，直接右移

对于有符号的被除数，先加上[除数-1]，再进行右移

无符号（正2的次幂）

用到了两个公式:

被除数 < 0时 向上取整 = 向下取整 + 1
被除数 < 0时 向上取整 = 向下取整(被除数 + (2^n)-1)

// 1. n / 8
(n + [(2^3) - 1|0]) >> 3 // n 为正数 +0 否则 + (2^3) - 1
// 2. n / 8
n >> 3 + [1|0] // n为正数 +0 否则 +1

需要使用向下取整构造出向零取整的表达式。

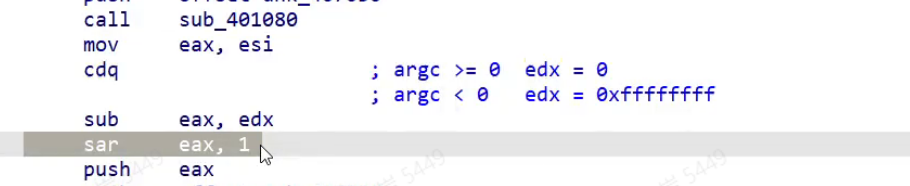
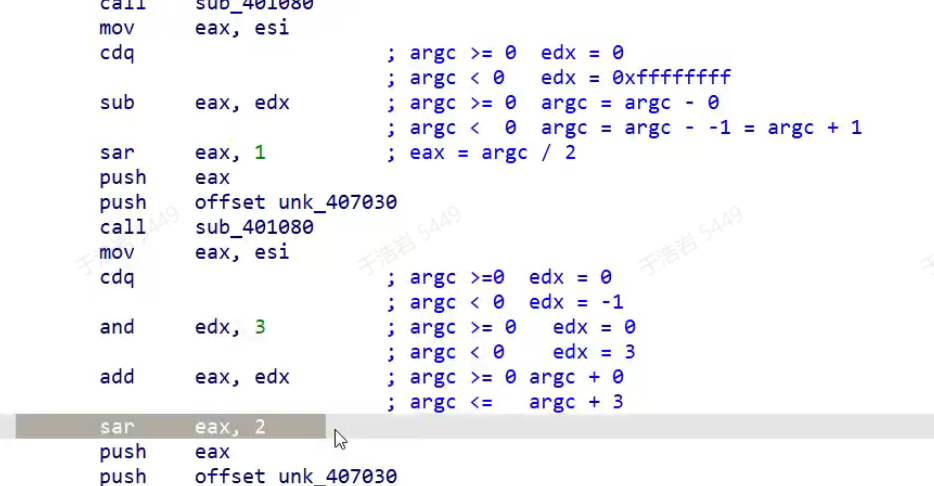
; printf("n1 / 2 = %d", n1 / 2);
mov     esi, DWORD PTR _n1$[esp]
mov     eax, esi
cdq                ; 使用eax的符号位拓展edx
                ; 如果eax是负数, edx = -1 如果是正数 edx = 0
sub     eax, edx         ; eax -= edx 如果eax是负数，相当于eax + 1 完成了加一操作
sar     eax, 1           ; 右移一位(向下取整)
push    eax
push    OFFSET `string'
call    _printf

;  printf("n1 / 8 = %d", n1 / 8);
mov     eax, esi
cdq
and     edx, 7        ; 构造 2^n - 1
add     eax, edx      ; 加上这个数
sar     eax, 3
push    eax
push    OFFSET `string'
call    _printf
add     esp, 24

Clang

test    ebx, ebx
lea     esi, [rbx+7]
mov     edi, OFFSET FLAT:.LC2
cmovns  esi, ebx
xor     eax, eax
sar     esi, 3
call    printf

test    ebx, ebx
lea     esi, [rbx+1023]
mov     edi, OFFSET FLAT:.LC3
cmovns  esi, ebx
xor     eax, eax
sar     esi, 10
call    printf

可以看到Clang也是使用先加法，再右移的优化方式。

有符号（负2的次幂）

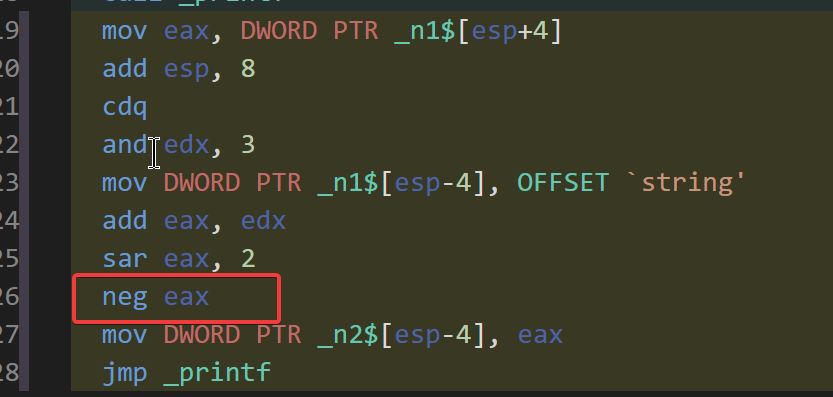
和正2的次幂一样，只是最后多了一个neg取反。

printf("%d", n1 / -4);

非2次幂除法

核心思想是：将带有常量的除法，优化为乘法。

x/c等价于x*c的倒数，那么

无符号除法

无误差

n:编译器选择，一般大于32\\ c:由编译器提前计算出的Magic Number\\ \frac{x}{c}=x\frac{1}{c}=x\frac{1*2^n}{c*2^n}=x\frac{2^n}{c}\frac{1}{2^n}\\ 设M=\frac{2^n}{c},最终得:\\ \frac{x}{c}=\frac{x*M}{2^n}\\ \\ 对于编译器来说:x\frac{2^n}{c}\frac{1}{2^n}\Rightarrow x*M >>n\\ 逆向时还原c:c=\frac{2^n}{M}

; printf("%u", n1 / 3)
mov eax, -1431655765 ; aaaaaaabH Magic Number 转换为无符号为=2863311531
mul DWORD PTR _n1$[esp-4]
shr edx, 1
push edx
push OFFSET `string'
call _printf

计算过程

对于M=2863311531先进行一次无符号乘法(mul)。
shr edx, 1，分两步，先取出结果中的低32位(进行右移32位)；再让结果右移1位。如此总共是33次右移，n=33。
完成了 $x*M >>n$ 的计算

还原除数

使用 $c=\frac{2^n}{M}$ 公式计算
$8589934592 ÷ 2863311531 = 2.9999999996507540345598531381041$ ，认为除数是3，且使用无符号乘法。
最终结果为uint32_t x = n1 / 3

有误差(除7优化)

对于无符号整数除法，编译器通过 Magic Number 和移位操作实现优化。虽然 3 和 7 都是小的非 2 的幂次的除数，但它们的 Magic Number 的误差范围不同，导致优化策略的差异。

3 的 Magic Number
- 倒数：1/3 ≈ 0.333333...
- Magic Number：ceil(2^32 / 3) = 1431655765 (0xAAAAAAAB)
- 误差：1431655765 / 2^32 - 1/3 ≈ 0（非常接近真实值）
7 的 Magic Number
- 倒数：1/7 ≈ 0.142857...
- Magic Number：ceil(2^32 / 7) = 613566757 (0x24924925)
- 误差：613566757 / 2^32 - 1/7 ≈ 0.00000001（误差更大）

结论： 3 的 Magic Number 几乎是精确的，因此不需要额外修正。而 7 的 Magic Number 误差较大，必须通过修正步骤来调整计算结果。

\cfrac{val}{c}=x\cfrac{1}{c}=x\cfrac{2^{32} + \cfrac{2^{32+n}}{c} - 2^{32}}{2^{32+n}}\\ 编译器企图用多次运算来减少精度的丢失，我们来看看此时如何计算c\\ 设M=\cfrac{2^{32+n}}{c} - 2^{32}\\ 则c=\cfrac{2^{32+n}}{2^{32} + M}

注意化简后的公式中包含了2^35大数，无法直接运用到代码，仍需使用第一步的公式

; val / 7
mov eax, 613566757 ; 24924925H
mul esi            ; val * M
sub esi, edx      ; val - (val * M /2^32) = IR1
shr esi, 1        ; IR1 >> 1 = IR2
add esi, edx      ; IR2 + val = IR3
shr esi, 2        ; IR3 >> 2 = result

还原除数

M=613566757, n=3
(2^(32+n)) =34359738368
2^32 + M = 4,908,534,053
带入公式 $c=\cfrac{2^{32+n}}{2^{32} + M}$
34359738368 ÷ 4908534053 =6.99999999938881

除数有符号

除数为正数

M < 80000000H

\frac{x}{c}=(x*M)>>n + \alpha\\ 当c\geqq0则\alpha=1\\ c<0则\alpha=0\\ 逆向时还原c:c=\frac{2^n}{M}

; 有符号 n1 / 3
mov eax, 1431655766 ; 55555556H
imul DWORD PTR _n1$[esp-4] ; 有符号
mov eax, edx
shr eax, 31 ; 0000001fH
add eax, edx

M=1431655766
2^32 / M = 2.9999999986030161387273035297509
c = 3

M > 7FFFFFFF

在进行有符号除法时，如果M>7FFFFFFF符号会被忽略。因为编译器在提前计算M的时候，采用的是无符号，也就是说M在进行imul的时候，被强制减去了2^32。

原本的公式为:\frac{x}{c}=x\frac{2^n}{c}\frac{1}{2^n}，M=\frac{2^n}{c}\\ 但是有符号除法强制忽略的最高位，导致M=M-2^{32}，公式变为:\\ \frac{x}{c}=x(\frac{2^n}{c}-2^{32})\frac{1}{2^n}=(x(\frac{2^n}{c}-2^{32})+x2^{32})\frac{1}{2^n}\\ 所以要在乘法之后先进行一次+x2^{32}的调整\\ 逆向时还原c:c=\frac{2^n}{M}

; int arg / 7
mov     eax, -1840700269              ; 92492493H
imul    esi        ; 结果为 edx : eax
add     edx, esi    ; 调整。edx是高32位，高32位+x等价于+x2^32
sar     edx, 2      ; 右移
mov     eax, edx
shr     eax, 31                             ; 0000001fH
add     eax, edx

M=92492493H=2,454,267,027
n=2+32 = 34
2^34 = 17,179,869,184
c = 6.999999997962731868

除数为负数

M < 80000000H

比较简单，反向调整，乘法之后减去一个 $x2^{32}$ 。

\frac{x}{c}=-\frac{x}{p}，p是c的补码\\ 上式变为-(x*\frac{2^n}{p}*\frac{1}{2^n})=(x*(-(\frac{2^n}{p}-2^{32}))-x*2^{32})\\ 可以和之前调整的差异，这里减去一个x*2^{32}\\ 逆向时还原c:c=\frac{2^n}{2^{32}-M}

; int / -7
mov     eax, 1840700269                     ; 6db6db6dH
imul    esi
sub     edx, esi      ; -x * 2^32
sar     edx, 2
mov     eax, edx
shr     eax, 31                             ; 0000001fH
add     eax, edx

M=1840700269
n=2+32 = 34
2^34 = 17,179,869,184
c = 2^34/2^32-M = 17,179,869,184 / 2,454,267,027 = 6.999999997
除数为-7

M > 7FFFFFFF

除数已经为负数了，此时M也为负数，正常情况用之前的公式再进行一次neg就可以得出结果，但是编译器使用另一种优化方式。

\frac{x}{c}=x*M*\frac{1}{2^{n}}\\ 当c<0时，M=-\frac{2^n}{|c|}=求补\frac{2^n}{|c|}=2^{32}-\frac{2^n}{|c|}\\ 逆向还原c:c=\frac{2^{n}}{2^{32}-M}

; int / -5
mov     eax, -1717986919              ; 99999999H
imul    esi            ; x * M
sar     edx, 1          ; *1/2^n
mov     eax, edx
shr     eax, 31                             ; 0000001fH
add     eax, edx

M=2,576,980,377
n=32 + 1 = 33
2^32 - M = 1,717,986,919
c = 2^33/2^32 - M = 4.9999999982